Mengerjakan Soal untuk mencari Determinan Matriks, Matriks
Minor, dan Matriks Kofaktor Ordo 4x4
Soal
Cari nilai Determinan Matriks, Matriks Minor, dan Matriks Kofaktor dari soal dibawah ini
Jawaban
:
a. Determinan Matriks
|A| = A1 + A2 + A3
1. Menghitung A1 (Pola 1 – 1 - 1)
A1 = (2.1.1.2) – (2.1.2.1) + (3.3.2.1) - (2.3.2.2) - (2.3.1.1) + (2.3.2.2) – (3.1.2.2) + (2.1.2.1)
A1 = 4 – 4 + 18 – 24 – 6 + 24 – 12 + 4
A1 = 4
2.
Menghitung
A2 (Pola 1 – 2 - 3)
A2 = - (2.1.2.2) + (2.1.2.2) - (3.3.2.1) + (2.3.1.1) + (2.3.2.2) - (2.3.1.2) + (3.1.2.1) - (2.1.2.1)
A2 = - 8 + 8 – 18 + 6 + 24 – 12 + 6 - 4
A2 = 2
3.
Menghitung
A3 (Pola 2 – 1 - 2)
A3 = (2.1.2.1) – (2.3.2.2) + (3.3.2.2) - (2.1.1.1) - (2.1.2.2) + (2.3.1.1) – (3.3.2.1) + (2.1.2.2)
A3 = 4 – 24 + 36 – 2 – 8 + 6 – 18 + 8
A3 = 2
Determinan
A
|A| = A1 + A2 + A3
|A| = 4 + 2 + 2
|A| = 8
Maka nilai determinan dari Matriks A adalah 8
b. Matriks Minor
a. c. Matriks
Kofaktor
Nahh.. sudah selesaii
Jika ada yang kurang jelas silahkan ditanya di kolom komentar..
see you..

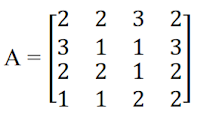



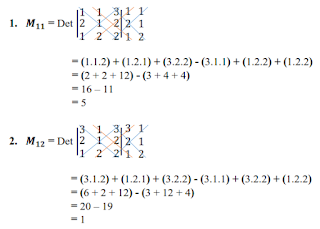
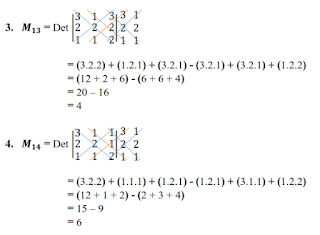











0 Comments